Eratosthenes
Eratosthenes of Cyrene (Greek: Ἐρατοσθένης, IPA: [eratostʰénɛːs]; English: /ɛrəˈtɒsθəniːz/; c. 276 BC[1] – c. 195 BC[2]) was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.
 He was the first person to use the word "geography" and invented the discipline of geography as we understand it.[3] He invented a system of latitude and longitude.
He was the first person to use the word "geography" and invented the discipline of geography as we understand it.[3] He invented a system of latitude and longitude.
He was the first person to calculate the circumference of the earth by using a measuring system using stades, or the length of stadiums during that time period (with remarkable accuracy). He was the first to calculate the tilt of the Earth's axis (also with remarkable accuracy). He may also have accurately calculated the distance from the earth to the sun and invented the leap day.[4] He also created a map of the world based on the available geographical knowledge of the era. In addition, Eratosthenes was the founder of scientific chronology; he endeavored to fix the dates of the chief literary and political events from the conquest of Troy.
According to an entry[5] in the Suda (a 10th century reference), his contemporaries nicknamed him beta, from the second letter of the Greek alphabet, because he supposedly proved himself to be the second best in the world in almost every field.[6]
Life
Eratosthenes studied in Alexandria, and claimed to have also studied for some years in Athens. In 236 BC he was appointed by Ptolemy III Euergetes I as librarian of the Alexandrian library, succeeding the second librarian, Apollonius of Rhodes, in that post.[7] He made several important contributions to mathematics and science, and was a good friend to Archimedes. Around 255 BC he invented the armillary sphere. In On the Circular Motions of the Celestial Bodies, Cleomedes credited him with having calculated the Earth's circumference around 240 BC, using knowledge of the angle of elevation of the sun at noon on the summer solstice in Alexandria and on Elephantine Island near Syene (now Aswan, Egypt).
Eratosthenes criticized Aristotle for arguing that humanity was divided into Greeks and barbarians, and that the Greeks should keep themselves racially pure, believing there was good and bad in every nation.[8] By 195 B.C., Eratosthenes became blind. He died in 194 B.C., at the age of 82.
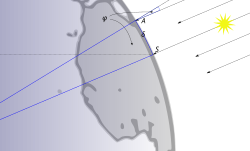
Eratosthenes' measurement of the Earth's circumference
Eratosthenes calculated the circumference of the Earth without leaving Egypt. Eratosthenes knew that on the summer solstice at local noon in the Ancient Egyptian city of Swenet (known in Greek as Syene, and in the modern day as Aswan) on the Tropic of Cancer, the sun would appear at the zenith, directly overhead (he had been told that the shadow of someone looking down a deep well would block the reflection of the Sun at noon). He also knew, from measurement, that in his hometown of Alexandria, the angle of elevation of the sun was 1/50th of a circle (7°12') south of the zenith on the solstice noon. Assuming that the Earth was spherical (360°), and that Alexandria was due north of Syene, he concluded that the meridian arc distance from Alexandria to Syene must therefore be 1/50 = 7°12'/360°, and was therefore 1/50 of the total circumference of the Earth. His knowledge of the size of Egypt after many generations of surveying trips for the Pharaonic bookkeepers gave a distance between the cities of 5000 stadia (about 500 geographical miles or 800 km). This distance was corroborated by inquiring about the time that it takes to travel from Syene to Alexandria by camel. He rounded the result to a final value of 700 stadia per degree, which implies a circumference of 252,000 stadia. The exact size of the stadion he used is frequently argued. The common Attic stadion was about 185 m,[9] which would imply a circumference of 46,620 km, i.e. 16.3% too large. However, if we assume that Eratosthenes used the "Egyptian stadion"[10] of about 157.5 m, his measurement turns out to be 39,690 km, an error of less than 2%.[11]
Although Eratosthenes' method was well founded, the accuracy of his calculation was limited. The accuracy of Eratosthenes' measurement would have been reduced by the fact that Syene is slightly north of the Tropic of Cancer, is not directly south of Alexandria, and the sun appears as a disk located at a finite distance from the Earth instead of as a point source of light at an infinite distance. There are other sources of experimental error: the greatest limitation to Eratosthenes' method was that, in antiquity, overland distance measurements were not reliable, especially for travel along the non-linear Nile which was traveled primarily by boat. Given the margin of error for each of these aspects of his calculation, the accuracy of Eratosthenes' size of the Earth is surprising.
Eratosthenes' experiment was highly regarded at the time, and his estimate of the Earth's size was accepted for hundreds of years afterwards. His method was used by Posidonius about 150 years later.
Other astronomical distances
Eusebius of Caesarea in his Preparatio Evangelica includes a brief chapter of three sentences on celestial distances (Book XV, Chapter 53). He states simply that Eratosthenes found the distance to the sun to be "σταδίων μυριάδας τετρακοσίας και οκτωκισμυρίας" (literally "of stadia myriads 400 and 80,000") and the distance to the moon to be 780,000 stadia. The expression for the distance to the sun has been translated either as 4,080,000 stadia (1903 translation by E. H. Gifford), or as 804,000,000 stadia (edition of Edouard des Places, dated 1974–1991). The meaning depends on whether Eusebius meant 400 myriad plus 80,000 or "400 and 80,000" myriad.
This testimony of Eusebius is dismissed by the scholarly Dictionary of Scientific Biography. It is true that the distance Eusebius quotes for the moon is much too low (about 144,000 km) and Eratosthenes should have been able to do much better than this since he knew the size of the earth and Aristarchus of Samos had already found the ratio of the moon's distance to the size of the earth. But if what Eusebius wrote was pure fiction, then it is difficult to explain the fact that, using the Greek, or Olympic, stadium of 185 m, the figure of 804 million stadia that he quotes for the distance to the sun comes to 149 million kilometres. The difference between this and the modern accepted value is less than 1%.[12] Scribal errors in copying the numbers, either of Eusebius' text or of the text that Eusebius read, are probably responsible.
The smaller of the foregoing two readings of Eusebius (4,080,000 stadia) turns out to be exactly 100 times the terrestrial radius (40,800 stadia) implicit in Eratosthenes' Nile map and given in the 1982 paper by Rawlins (p. 212) that analysed this map (see Further Reading). Greek scholars such as Archimedes and Posidonius normally expressed the sun's distance in powers of ten times the Earth's radius. The Nile map – Eusebius consistency is developed in a 2008 Rawlins paper. The data would make Eratosthenes' universe the smallest known from the Hellenistic era's height, and made the sun smaller than the earth. His indefensible lunar distance would require the moon to go retrograde among the stars every day for observers in tropical or Mediterranean latitudes, and would predict that half moons occur roughly 10° from quadrature.
The Eusebius-confirmed 1982 paper's empirical Eratosthenes circumference (256,000 stadia instead of 250,000 or 252,000 as previously thought) is 19% too high. But the 2008 paper notes that the theory that atmospheric refraction exaggerated his measurement (a theory originally proposed in the 1982 paper, applied to either mountaintop dip or lighthouse visibility) is thus bolstered as the explanation of Eratosthenes' error. This is because accurately measuring the visibility distance of the Alexandria lighthouse (then world's tallest, built at Eratosthenes' location and during his time) and computing the Earth's size from that should have given a result 20% high from refraction, very close to his actual 19% error. The 2008 paper wonders if the 40,800 stadia estimate originated with Sostratus of Cnidus (who designed the lighthouse), and offers a reconstructive speculation that the lighthouse was about 93 meters high, which is much below previous suppositions.
Prime numbers
Eratosthenes also proposed a simple algorithm for finding prime numbers. This algorithm is known in mathematics as the Sieve of Eratosthenes.
Works
- Περὶ τῆς ἀναμετρήσεως τῆς γῆς (On the Measurement of the Earth)[13] (lost, summarized by Cleomedes)
- Geographica (lost, criticized by Strabo)
- Arsinoe (a memoir of queen Arsinoe; lost; quoted by Athenaeus in the Deipnosophistae)
- A fragmentary collection of Hellenistic myths about the constellations, called Catasterismi (Katasterismoi), was attributed to Eratosthenes, perhaps to add to its credibility.
Named after Eratosthenes

- Eratosthenes (crater) on the moon
- Eratosthenian period in the lunar geologic timescale
- Eratosthenes Seamount in the eastern Mediterranean Sea
See also
Notes
- ^ The Suda states that he was born in the 126th Olympiad, (276–272 BC). Strabo (Geography, i.2.2), though, states that he was a "pupil" (γνωριμος) of Zeno of Citium (who died 262 BC), which would imply an earlier year-of-birth (c. 285 BC) since he is unlikely to have studied under him at the young age of 14. However, γνωριμος can also mean "acquaintance," and the year of Zeno's death is by no means definite. Cf. Eratosthenes entry in the Dictionary of Scientific Biography (1971)
- ^ The Suda states he died at the age of 80, Censorinus (De die natali, 15) at the age of 81, and Pseudo-Lucian (Makrobioi, 27) at the age of 82.
- ^ Erastothenes (2010). Eratosthenes' "Geography". Fragments collected and translated, with commentary and additional material by Duane W. Roller. Princeton University Press. ISBN 978-0691142678.
- ^ Alfred, Randy (June 19, 2008). "June 19, 240 B.C.: The Earth Is Round, and It's This Big". Wired. http://www.wired.com/science/discoveries/news/2008/06/dayintech_0619.
- ^ Entry ε 2898
- ^ See also Asimov, Isaac. Asimov's Biographical Encyclopedia of Science and Technology, new revised edition. 1975. Entry #42, "Eratosthenes", Page 29. Pan Books Ltd, London. ISBN 0-330-24323-3. It was also asserted by Carl Sagan, 31 minutes into his Cosmos episode The Shores of the Cosmic Ocean [1]
- ^ Oxford Reference (subscription required)
- ^ * p439 Vol. 1 William Woodthorpe Tarn Alexander the Great. Vol. I, Narrative; Vol. II, Sources and Studies0. Cambridge: Cambridge University Press, 1948. (New ed., 2002 (paperback, ISBN 0-521-53137-3)).
- ^ Engels, Donald (Autumn 1984). "The Length of Eratosthenes' Stade". American Journal of Philology 106 (3): 298–311. doi:10.2307/295030. JSTOR 295030.
- ^ Isaac Moreno Gallo (3–6 November 2004). "Roman Surveying" (PDF). Archived from the original on 2007-02-05. http://web.archive.org/web/20070205033538/http://traianus.rediris.es/topo01/surveying.pdf
- ^ There is a huge Eratosthenes-got-it-right literature based upon attacking the applicability of the standard 185 m stadium to his experiment. Among advocates: F. Hultsch, Griechische und Römische Metrologie, Berlin, 1882; E. Lehmann-Haupt, Stadion entry in Paulys Real-Encyclopädie, Stuttgart, 1929; I. Fischer, Q. Jl. R. astr. Soc. 16.2:152–167, 1975; Gulbekian (1987); Dutka (1993). The means employed include worrying various ratios of the stadium to the unstably defined "schoenus", or using a truncated passage from Pliny. (Gulbekian just computes the stadium from Eratosthenes' experiment instead of the reverse.) A disproportionality of literature exists because professional scholars of ancient science have generally regarded such speculation as special pleading and so have not bothered to write extensively on the issue. Skeptical works include E. Bunbury's classic History of Ancient Geography, 1883; D. Dicks, Geographical Fragments of Hipparchus, University of London, 1960; O. Neugebauer, History of Ancient Mathematical Astronomy, Springer, 1975; J. Berggren and A. Jones, Ptolemy's Geography, Princeton, 2000. Some difficulties with the several arguments for Eratosthenes' exact correctness are discussed by Rawlins in 1982b page 218 and in his Contributions and Distillate. See also, at [2], "The Shores of the Cosmic Ocean", chapter 1 of Cosmos: A Personal Voyage, a TV series by Carl Sagan, Ann Druyan and Steven Sotter (1978–1979), where a description of Eratosthenes' experiment is presented.
- ^ Other than the distance to the moon, no celestial distance is unambiguously established as known in antiquity even to within a factor of two. As late as a century ago, the earth's distance from the sun (the A. U.) was known less accurately than 16%.
- ^ Mentioned by Hero of Alexandria in his Dioptra. See p. 272, vol. 2, Selections Illustrating the History of Greek Mathematics, tr. Ivor Thomas, London: William Heinemann Ltd.; Cambridge, MA: Harvard University Press, 1957.
Further reading
- Bulmer-Thomas, Ivor (1939-1940). Selections Illustlating the History of Greek Mathematics. Cambridge, MA: Harvard University Press.
- Dorofeeva, A. V. (1988). "Eratosthenes (ca. 276–194 B.C.)" (in Russian). Mat. V Shkole (4): i.
- Dutka, J. (1993). "Eratosthenes' measurement of the Earth reconsidered". Arch. Hist. Exact Sci. 46 (1): 55–66. doi:10.1007/BF00387726.
- El'natanov, B. A. (1983). "A brief outline of the history of the development of the sieve of Eratosthenes" (in Russian). Istor.-Mat. Issled. 27: 238–259.
- Fowler, D. H.; Rawlins, Dennis (1983). "Eratosthenes' ratio for the obliquity of the ecliptic". Isis 74 (274): 556–562. doi:10.1086/353361.
- Fraser, P. M. (1970). "Eratosthenes of Cyrene". Proceedings of the British Academy 56: 175–207.
- Fraser, P. M. (1972). Ptolemaic Alexandria. Oxford: Clarendon Press.
- Goldstein, B. R. (1984). "Eratosthenes on the "measurement" of the earth". Historia Math. 11 (4): 411–416. doi:10.1016/0315-0860(84)90025-9.
- Gulbekian, E. (1987). "The origin and value of the stadion unit used by Eratosthenes in the third century B.C". Arch. Hist. Exact Sci. 37 (4): 359–363. doi:10.1007/BF00417008.
- Knaack, G. (1907). "Eratosthenes". Pauly–Wissowa VI: 358–388.
- Manna, F. (1986). "The Pentathlos of ancient science, Eratosthenes, first and only one of the "primes"" (in Italian). Atti Accad. Pontaniana (N.S.) 35: 37–44.
- Muwaf, A.; Philippou, A. N. (1981). "An Arabic version of Eratosthenes writing on mean proportionals". J. Hist. Arabic Sci. 5 (1–2): 174–147.
- Nicastro, Nicholas (2008). Circumference: Eratosthenes and the ancient quest to measure the globe. New York: St. Martin's Press. ISBN 0312372477.
- O'Connor, John J.; Robertson, Edmund F., "Eratosthenes", MacTutor History of Mathematics archive, University of St Andrews, http://www.history.mcs.st-andrews.ac.uk/Biographies/Eratosthenes.html.
- Pfeiffer, Rudolf (1968). History of Classical Scholarship From the Beginnings to the End of the Hellenistic Age. Oxford: Clarendon Press.
- Rawlins, D. (1982). "Eratosthenes' geodesy unraveled : was there a high-accuracy Hellenistic astronomy". Isis 73: 259–265. doi:10.1086/352973.
- Rawlins, D. (1982). "The Eratosthenes – Strabo Nile map. Is it the earliest surviving instance of spherical cartography? Did it supply the 5000 stades arc for Eratosthenes' experiment?". Arch. Hist. Exact Sci. 26 (3): 211–219.
- Rawlins, D. (2008). "Eratothenes's large earth and tiny universe" (PDF). DIO 14: 3–12. http://www.dioi.org/vols/we0.pdf.
- Roller, Duane W. (2010). Eratosthenes' Geography: Fragments collected and translated, with commentary and additional material. Princeton: Princeton University Press. ISBN 9780691142678. http://books.google.com/books?id=8peKyWK_SWsC.
- Strabo (1917). The Geography of Strabo. Horace Leonard Jones, trans. New York: Putnam.
- Taisbak, C. M. (1984). "Eleven eighty-thirds. Ptolemy's reference to Eratosthenes in Almagest I.12". Centaurus 27 (2): 165–167. Bibcode 1984Cent...27..165T. doi:10.1111/j.1600-0498.1984.tb00766.x.
- Wolfer, E. P. (1954). Eratosthenes von Kyrene als Mathematiker und Philosoph. Groningen-Djakarta.
External links
- Bernhardy, Gottfried: "Eratosthenica" Berlin 1822 Reprinted Osnabruck 1968 (German text)
- Bernhardy, Gottfried: Eratosthenica Berlin, 1822 (PDF) (Latin/Greek)
- Eratosthenes' sieve in Javascript
- Eratosthenes' sieve as a simple algorithm
- About Eratosthenes' methods, including a Java applet
- How to measure the earth with Eratosthenes' method
- How the Greeks estimated the distances to the moon and sun
- Eratosthenes on PBS.org
- Measuring the earth with Eratosthenes' method
- List of ancient Greek mathematecians and contemporaries of Eratosthenes
- New Advent Encyclopedia article on the Library of Alexandria
- Eratosthenes' sieve explored and visualised in Flash
- Eratosthenes' sieve in classic BASIC all-web based interactive programming environment
- Following in the footsteps of Eratosthenes : project fr:La main à la pâte.